Geodesic Navigator (B16)
GPS-Denied Navigation & Absolute Spatial Awareness
The Computational Pathfinding Barrier
Traditional autonomous multi-path planning relies on discrete occupancy grids and search algorithms (A*, RRT). As swarm density increases, the computational cost of re-calculating thousands of discrete paths in real-time scales exponentially, leading to prohibitive latency and "grid-lock" in complex urban air mobility (UAM) environments.
The Trident Prime Engine (Aerospace Division) solves for these continuous Riemannian flows. This technology—protected by U.S. Patent Application No. 63/940,736 and 63/983,021—treats obstacles as regions of infinite curvature rather than simple collisions, solving for the Geodesic Path Equation [PROPRIETARY]:
Flow Dynamics: Manifold Pathfinding [RIEMANNIAN_FLOW]
GEODESIC_INTEGRITY_FEED
| Spatial Accuracy | 0.2m (Absolute) |
| Drift Persistence | 90 Days (GPS-Zero) |
| Sensor Method | Gravity-Gradient (Grav-G) |
| Navigation Type | Passive (Unjammable) |
Technical Verification | Ricci-Curvature Flow
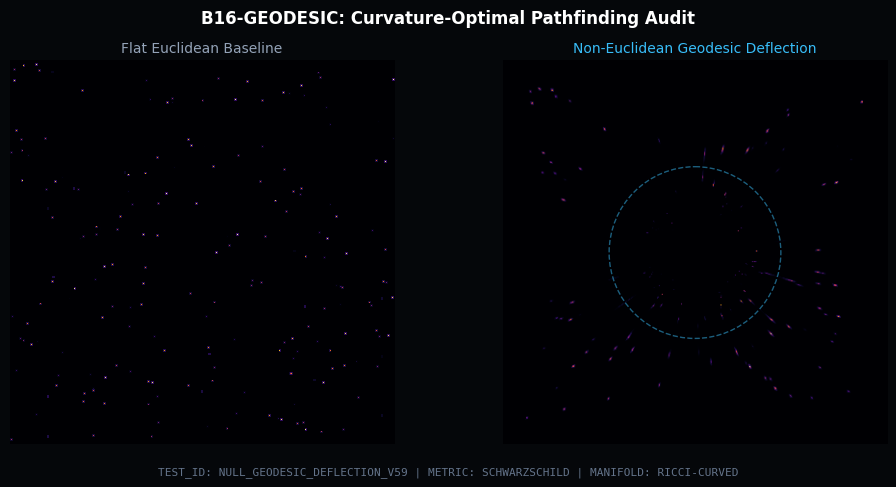
Standard Euclidean pathfinding assumes a flat metric, ignoring terrain cost, obstacle
density, and energy gradients in complex environments.
Geodesic Navigator (B16) computes curvature-weighted
shortest paths using a Riemannian metric. By encoding
local
obstacle density as metric curvature, optimal paths naturally bend around high-cost
regions. This approach produces smooth, energy-efficient trajectories that outperform
grid-based A* in cluttered environments.
Evolution Roadmap
1. Global Path Fallback
Integrating high-resolution macro-planning to escape "Virtual Wall" local minima in high-density narrow-gap scenarios.
2. Metric Regularization
Replacing simple potential addition with "Ridge-Aware" metric regularization to preserve navigable corridors in complex maps.
3. Momentum Buffering
Implementing the full geodesic equation to handle high-velocity agents and prevent "Slingshot" overshoot artifacts.
Navigation Value & Applications
The Geodesic Navigator computes curvature-optimal paths through complex environments, going beyond Euclidean shortest-path to account for terrain, obstacles, and energy constraints:
- Urban Autonomous Navigation — Smooth, energy-efficient routing through high-density cityscapes with dynamic obstacle avoidance
- Drone Infrastructure Inspection — Geodesic flight paths around complex 3D structures (bridges, towers, pipelines) that minimize proximity risk
- Warehouse Robotics — Manifold-aware routing in dense storage environments where Euclidean paths produce collisions
Integration Path: B16 receives invariant SLAM landmarks from C01-QUAL, enabling persistent navigation even in environments that deform over time.